材料力学の基礎として、引張応力、せん断応力、ポアソン比について説明
1. はじめに
今回から私の専門である機械工学について、復習と備忘録的な目的で記事として残していければと思います。
将来的には、仕事で必要としている人、自主学習、大学のテスト勉強、大学院の入試対策などに使って頂けるくらい充実した内容にできればと思っています。
今回はまずPart1ということで、材料力学の概要を説明できればと思います。
2. 材料力学とは
材料力学とは、機械工学における四力(材料力学、熱力学、流体力学、機械力学)の1つで、材料の変形や破壊などを扱う学問です。
高校物理との違いについてですが、高校物理で扱う物体は剛体と仮定されています。つまり「対象物の変形は無視できるかまたは全く変形しない」と仮定して問題を解いてるわけです。
しかし実際の物体は力が掛かれば変形するし破壊します。では変形量は?変形しても性能を発揮できる?壊れないためにはどんな材料を選べば良い?寸法は?といった課題を解決するのが材料力学になります。
実用上はさらに動的負荷といって疲労やクリープなんかも考えなければいけませんが、こちらは今後説明できればと思います。
材料力学は様々な分野で使用されており、機械工学だけでなく土木系や建築系でも習います。物を作る場合は応力設計が必要になるため、材料力学に長けている技術者は現場で非常に重宝されます。
3. 説明
3.1 引張応力
まず応力の定義について説明します。専門書によって微妙にニュアンスが違うことがありますが、「物体が外力を受ける時、物体内の任意の断面に分布している単位面積あたりの内力を応力という」と定義されています。
例えば以下のように片端固定の物体に引っ張りの外力Wが作用して、かつ静止している状態を考えます。

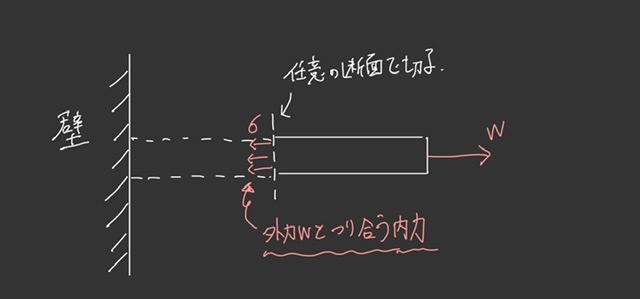
物体が静止している(平衡状態)ので力が釣り合っていないといけません。
つまり材料の任意の断面で切っても必ず外力Wと内力が釣り合っていることになります。
この内力を断面積で割った値を応力と言います。式は以下になります。
σ:応力、W:外力、A:断面積
また外力が作用した時、材料は変形します。上記の例では伸びる方向に変形します。
その時の応力と歪(伸びに関係する物理量)の関係は以下になります。この式をフックの法則と言います。
...(1)
σ:応力、E:ヤング率(縦弾性係数)、ε:ひずみ
歪みの定義式は以下になります。
...(2)
ε:ひずみ、λ;伸び、l:材料の初期長(外力が作用する前の長さ)
歪とはいわゆる膨張率(または圧縮率)の事だと思って問題ありません。
ちなみに(1)式と(2)式から伸びを求めると、
になります。この式変形は今後、自重による変形、ひずみエネルギーの導出で使ったり、大学のテスト等でも使うので覚えておきましょう。
3.2 せん断応力
さきほどの引張応力の例では、材料の断面に垂直に力が作用している場合を考えました。
しかし力は引っ張りだけではありません。皆さんはお菓子の袋を開ける時にどう開けますか?
「引っ張る」のではなくギザギザの部分を「ちぎって」開けると思います。この時の応力がせん断応力です。
以下のように貼り合わせた板を両側から引っ張る場合や軸をねじる場合などにせん断応力を考えます。
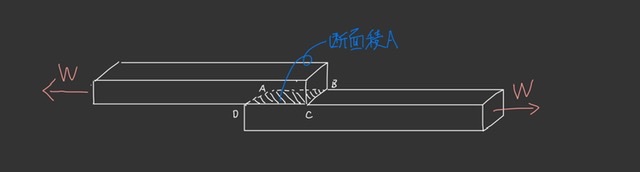
せん断応力の定義は以下になります。
τ:剪断応力、W:荷重、A:面積
ここでせん断応力の式は以下になります。
τ:剪断応力、G:横弾性係数、γ:せん断ひずみ
またせん断ひずみの式は以下になります。
γ:せん断ひずみ、λ:変形量、l:初期長
図で表すと以下になります。
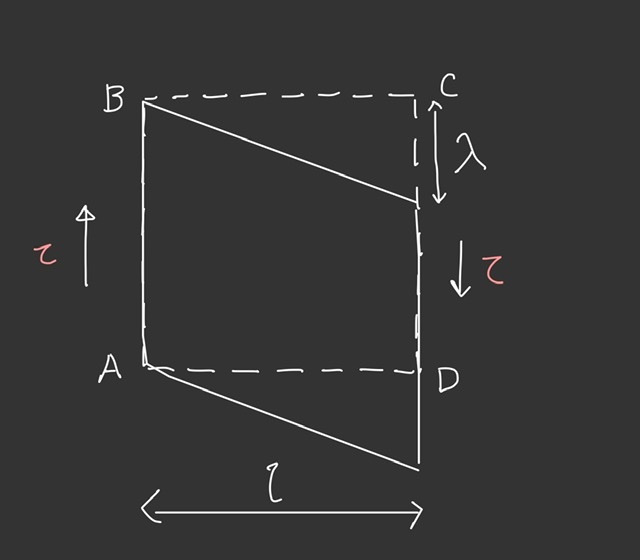
3.3 ポアソン比
最後にポアソン比について説明します。
3.1と同じ様に片端固定の物体に引張荷重Wが作用している状況を考えてみましょう。
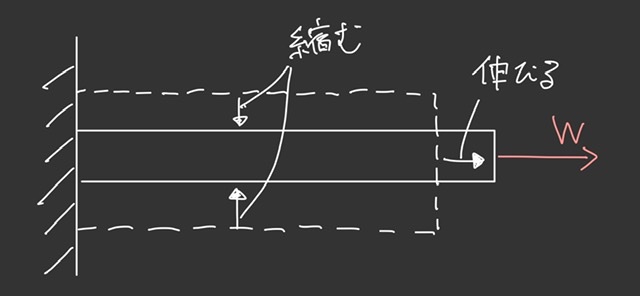
この時、軸方向(外力が掛かっている方向)には伸びますが、それ以外の方向は実は縮んでいます。ではどのくらい縮むのか?
それを表しているのがポアソン比です。
v:ポアソン比、ε1:力が掛かっている方向のひずみ(図では軸方向)、ε2:それ以外の方向のひずみ(図では幅の方向)
等方性材料のポアソン比は0.3前後が多いです。
3.4 実用上の小ネタ:単位について
通常、応力はMPa、ヤング率はGPa、寸法はmmで表します。
図面の寸法は基本的にmmです。また力はNが使われます。
そのため応力の定義:応力=力/面積を考えると、N/mm^2 = N/m^2 × 10^6 = Pa × 10^6 =MPaとなるため、MPaに慣れておくと計算しやすくなります。
また通常はMPa以下の応力はほとんど設計に関係なく、無視することもあります。
ヤング率は一般構造用鋼は206GPa、アルミは69GPaは良くテストで出るので覚えておくと良いです。
4. 例題(答えは次回)
4.1 引張応力について
Q: 直径10mm、長さ100mmの丸棒を20Nの力で引っ張った時の伸び量を求めなさい。ただし材質はアルミ(E=69GPa)とする
4.2 せん断応力
Q: 以下の図において、W=10kN、AB=5mm、BC=5mmの時、作用するせん断応力を求めろ。

5. 最後に
いかがだったでしょうか。
今回は材料力学の概要を説明しました。
次回はE,G,vの関係式や、応力歪み線図などを説明できればと思います。