【python】【tkinter】【part3】canvasを使って物理計算をする

tkinterのcanvasを使って斜めにボールを投げた時の飛距離を計算する

■はじめに

前回、tkinterのcanvasで図形を描く方法とその図形を動かす方法を紹介しました。

stjun.hatenablog.com

stjun.hatenablog.com

今回は前回の図形を動かす機能を使って、ボールを斜めに投げた時の挙動をcanvasを使ってシミュレーションしたいと思います。

■コード

import tkinter as tk
import time
import numpy as np

#ウインドを作成
root=tk.Tk()
root.geometry('400x400')
root.title('canvasの使い方')

#図形を壁画するキャンバスをウインド上に作成
canvas=tk.Canvas(root,width=300,height=300,bg="white")
canvas.pack()

#ボールの壁画
dx=20
dy=20
square=canvas.create_rectangle(5,5,5+dx,5+dy,fill='red')#四角

#動かすためのパラメータ
x=0#ボールの初期x座標
y=300-dy#ボールの初期y座標
seta=np.pi/4#ボールを投げる角度
V=30#ボールの初速度
Vx=V*np.cos(seta)#x軸方向の速度
Vy=-V*np.sin(seta)#y軸方向の速度
dt=0.001 #時間刻み
ay=9.81 #重力加速度
Y_current=300-dy #地面の位置（下端）

start=time.time() #開始時間
stop_time=10 #目標終了時間

#計算部分
while True:
    canvas.coords(square,x,y,x+dx,y+dy) #ボールを指定の座標に移動させる
    x+=abs(Vx)*dt #微小時間dtでx方向に動く量
    y+=Vy*dt #微小時間dtでy方向に動く量
    Vy+=ay*dt #微小時間dtにおけるy方向の速度の変化量
    root.update() #ウインド画面を更新
    
    #地面に接したら終了＋飛距離を計算
    if y>=Y_current:
        print('飛距離は',x,'[m]です')
        break

root.mainloop()

左下の角がスタート位置で、そこから右斜め（45°方向に初速30[m/s]）にボールを投げた時のシミュレーションを行います。

実行すると以下のように四角が動きます。

（今回も動画の載せ方が分からないので画像です）

また飛距離を計算したのが以下になります。

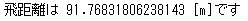
理論値が91.7431...なのでまあまあ近いですね。dtをもっと細かくしていけばより理論値に近づくはずです。（といってもこの程度なら計算した方が早いのでシミュレーションするほどでもないですが...笑）

■買って良かったもの紹介

 今回紹介したmatplotlib以外にもpandasやBokehなどのモジュールの使い方が書かれている本です。

公式リファレンス等もありますし、ネットで探せばいくらでもモジュールの使い方・書き方は見つかりますが、一冊くらいこのような本を手元に持っておくと便利です。

pythonを初めて触ろうとした時に読んだ本を紹介します。

 この本は、初心者に最適だと思います。確か亀を動かすゲームのようなコードが載っていたと思います。pythonをこれから始めようと思っている人は読んでみて下さい。

また下の入門python3も良い本だと思いますが、分厚いので中々根気が必要です。個人的には最小限必要なことが書いてある薄い本を読み、必要になってからちょっとずつ知識を増やしていくのが良いと思います。

また何度も紹介しますが、以下のニューラルネットワーク自作入門は非常に良い本です、pythonの書き方から記載されているのでいきなり読んでも大丈夫だと思います。

 とりあえず基本的なコードの書き方さえ分かってしまえば、後はネットで知りたい情報にアクセスする方が早いと思います。

■説明

 主に前回からの変更点は以下になります。

#計算部分
while True:
    canvas.coords(square,x,y,x+dx,y+dy) #squareを指定の座標に移動させる
    x+=abs(Vx)*dt
    y+=Vy*dt #縦方向に少しづつ動かす
    Vy+=ay*dt

距離＝速度×時間

速度＝加速度×時間

の式になっています。

より詳しく言うと、dx/dt=Vなので、dx/dt ≒ (x-x')/Δtと離散化すると（x'がt-1でのx座標,xがtでのx座標）、x=V×Δt+x'になります。つまり前回のx座標に速度×微小時間の値を足すと現在のx座標になるということです。

同様に加速度についても、dV/dt=aなので、dV/dt ≒ (V-V')/Δtと離散化すると（V'がt-1での速度,Vがtでの速度）、V=a×Δt+V'になります。

上記を詳しく知りたい方は数値計算の分野になるので調べてみて下さい。

よく非定常の熱伝導方程式を解く例や、反応速度を用いて化学種の計算をする時などに使われている気がします。

■おわりに

いかがだったでしょうか。次回はtkinterでGUIを作り、角度や初速度を変えられるようにしたいと思います。